この記事では、こんな疑問を解決しています。
- 本日の授業テーマ
- 本日の授業内容
※リンクをクリックすれば各項目へジャンプできます
この記事では「教科書よりもわかりやすい物理解説」をコンセプトに、高校物理を「基本のキ」から解説しています。
学校の授業で理解できなかったことを、ぜひこの記事で学び直してみて下さい!
それでは、レッツゴーッ!
この記事を書いている私は、受験指導歴8年の現役塾講師です。
出身は岩手県で、立命館大学に進学・卒業した後、大手塾講師として200人以上の中高生の勉強相談に答えてきました。
速度と加速度のおさらい|物理基礎(力学)
前回の記事では「速度」と「加速度」の定義・考え方について解説しました。
(まだ見てない人はぜひ見てね↓)
上の記事の要点だけをまとめると、こうなります。
$$\boldsymbol{v=\frac{Δx}{Δt} \, [m/s]}$$
$$\boldsymbol{a=\frac{Δv}{Δt} \, [m/s^2]}$$
- 速度・・・物体の位置が、1秒間でどれくらい変化するかを表す量
- 加速度・・・物体の速度が、1秒間でどれくらい変化するかを表す量
速度と加速度の違いを明確に意識しておけば、「加速度は$ー$だけど速度は$+$」といった状況にも、問題なく対応できるはず。
速度と加速度の定義・考え方は、等加速度直線運動を学ぶうえでも必須の知識です。
あやふやなままにせず、しっかり理解してから先に進むと良きですよ。
等加速度直線運動の重要公式3つ|物理基礎(力学)
等加速度直線運動とは「加速度$\boldsymbol{\,a \,}$が一定な直線運動」のコト。
今回紹介する重要公式は次の3つです。
- $\boldsymbol{v=v_0 \, +at}$
- $\boldsymbol{x=v_0 \, t+\dfrac{1}{2}at^2}$
- $\boldsymbol{v^2-v_0^2=2ax}$
※$ \, v_0 \, $・・・初速度
式だけ見てもなんのこっちゃだと思うので、一つ一つ丁寧に解説していきますね。
$\boldsymbol{v=v_0 \, +at} \,$の解説
初めに「加速度がない運動」について考えてみます。
加速度がない物体の$ \, t \,$秒後の速度は、もちろん
$$v=v_0$$
これをを$\,v-t\,$グラフにするとこうなります。

続いて「加速度のある運動」について考えてみます。
加速度とは「1秒間に変化する速度」を表す量でしたよね。
$a=10 \, m/s^2 \, $なら、「1秒間に$10 \, m/s \, $ずつ速度が増加する」ということ。
よって、加速度のある物体の$ \, t \, $秒後の速度は
$$\boldsymbol{\color{red}v=v_0 \, +at}$$
以上が1つめの公式の成り立ちです。
$\,v-t\,$グラフするとこう↓
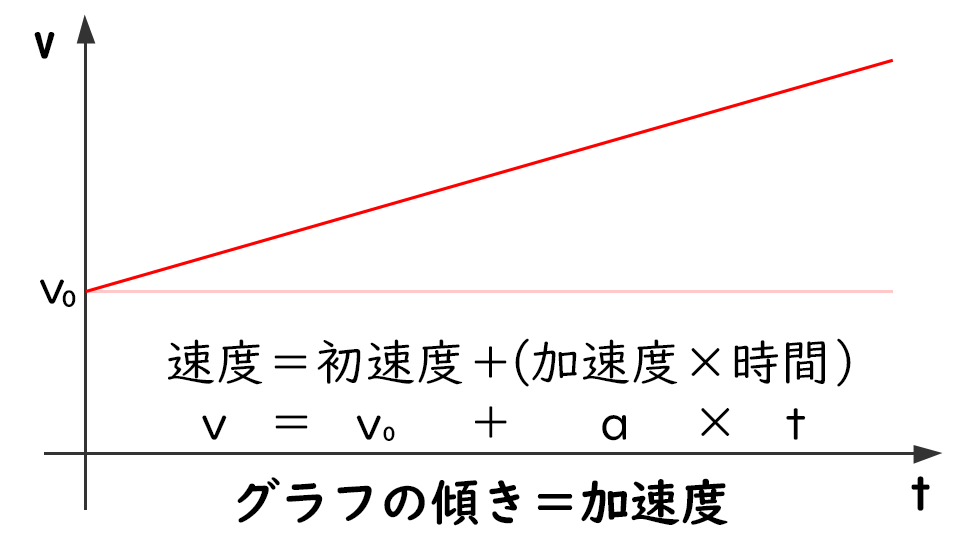
初速度$\,v_0\,=5\,m/s\,$、加速度$\,a=2\,m/s\,$で等加速度運動をする物体がある。
$\,t=10s\,$のときの物体の「速度」と「加速度」を求めてみよう!
※動き始めを$\,t=0s\,$とする
公式$\,v=v_0 \, +at\,$より、
$$v=5+(2\times10)$$
$$\color{red}v=25\,[m/s]$$
また、この物体は等加速度運動をしているため、加速度は一定。
よって加速度は$\color{red}\,a=2\,[m/s^2]$
$\boldsymbol{x=v_0 \, t+\dfrac{1}{2}at^2} \,$の解説
初めに「加速度がない運動」について考えてみます。
加速度$ \, a=0 \,$の物体が$ \, t \,$秒間で進む距離(変位)$ \, x \, $は、
$$x=v_0 \, \times \, t$$
これをグラフにするとこうなります。

続いて「初速度0で加速度だけある運動」について考えてみます。
初速度$ \, v_0=0 \, $で加速度$ \, a \,$のみがある場合、物体が$ \, t \,$秒間で進む距離(変位)$ \, x \, $は
$$x=\dfrac{1}{2} \, \times \, a \, \times \, t^2$$
式だけ見ると理解できないかもですが、グラフにすると割とカンタンでして
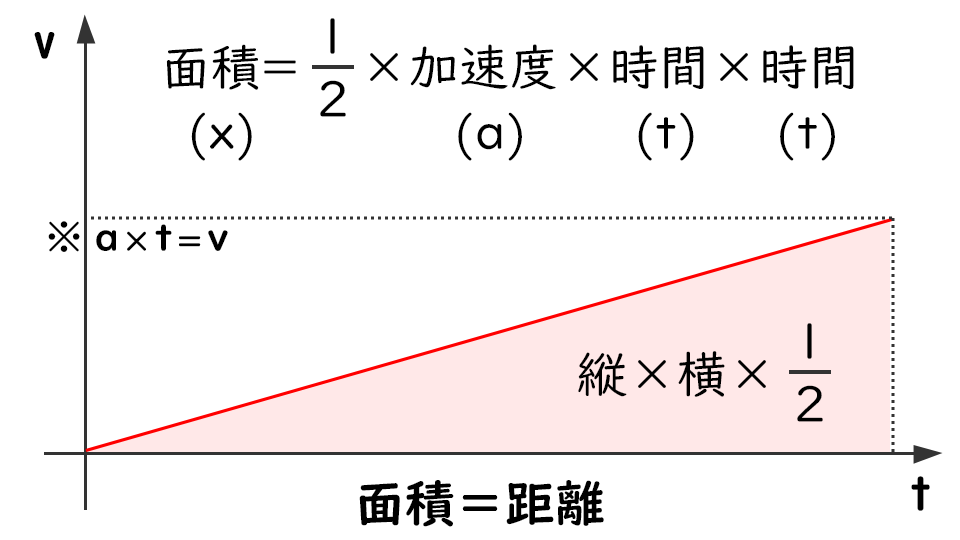
最後に「初速度も加速度もある運動」を考えます。
物体が$ \, t \, $秒間で進む距離は
$$\boldsymbol{\color{red}x=v_0 \, t+ \dfrac{1}{2}a \, t^2}$$
グラフにするとこう↓

初速度$\,v_0\,=5\,m/s\,$、加速度$\,a=2\,m/s\,$で等加速運動をする物体がある。
$\,t=10s\,$のときの物体の変位$\boldsymbol{\,x\,}$を求めてみよう!
※動き始めを$\,t=0s\,$とする
公式$\,x=v_0 \, t+ \dfrac{1}{2}a \, t^2$より、
$$x=5\times10+\dfrac{1}{2}\times2\times10^2$$
$$\color{red}x=150\,[m]$$
$\boldsymbol{v^2-v_0^2=2ax} \, $の解説
この公式は、ここまでに解説した2つの公式を組み合わせることで導くことができます。
\begin{eqnarray}\left\{\begin{array}{1}v=v_0 \, +at \, ・・・①\\x=v_0 \, t+\dfrac{1}{2}at^2 \, ・・・②\end{array}\right.\end{eqnarray}
①より
$$t=\dfrac{v-v_0}{a} \, ・・・①^´$$
$①^´$を②の$ \, t \, $に代入して
$$x=v_0\left( \dfrac{v-v_0}{a} \right)+\dfrac{1}{2}a \left( \dfrac{v-v_0}{a} \right)^2$$
$$x=\dfrac{v_0 \, \left( v-v_0 \right)}{a}+\dfrac{1}{2} \dfrac{ \left( v-v_0 \right)^2}{a}$$
両辺に$\, 2a \,$を掛けて
$$2ax=2v_0 \, \left( v-v_0 \right)+ \left( v-v_0 \right)^2$$
$$2ax=2v_0 \, v-2v_0^2+v^2-2v \, v_0 \, +v_0^2$$
$$\boldsymbol{\color{red}v^2-v_0^2=2ax} \, $$
初速度$\,v_0\,=5\,m/s\,$で等加速度運動を始めた物体がある。
物体の変位が$\,x=150m\,$になったときの速度が$\,v=25\,m/s\,$の場合、物体の加速度$\boldsymbol{\,a\,}$の値を求めよ。
公式$\,v^2-v_0^2=2ax$より、
$$25^2-5^2=2\times a\times150$$
$$\dfrac{600}{300}=a$$
$$\color{red}a=2\,[m/s^2]$$
等加速度直線運動の公式の使い分け|物理基礎(力学)
最後に一つ、「公式の使い分け」についてお話します。
「公式を使ってみよう!」のコーナーにおいて、最後の公式$\boldsymbol{\,v^2-v_0^2=2ax\,}$の問題だけ、少し毛色が違うことに気が付きましたか?


実は最後の問題だけ「時間$\,t\,$」を使わずに、解いているんです!

3つの公式を見比べてみると分かる通り、最後の公式の中には$\,t\,$が存在しないことが分かります。
- $\boldsymbol{v=v_0 \, +at}$
- $\boldsymbol{x=v_0 \, t+\dfrac{1}{2}at^2}$
- $\boldsymbol{v^2-v_0^2=2ax}$
※$ \, v_0 \, $・・・初速度
練習問題をいくつか解けば感覚がつかめてくるのですが、
時間に関係した問題では「1」と「2」、そうでなければ「3」の公式といった感じで使い分けると、スムーズに問題を解くことができます。



等加速度直線運動のまとめ|物理基礎(力学)
以上が、高校物理における「等加速度直線運動」の重要公式についての説明です。
数式が盛りだくさんで、やや疲れましたね(;^ω^)
繰り返しになりますが、今回紹介した3つの公式は今後何度もお世話になる重要な公式です。
自然と使いこなせるようになるまで、練習問題を繰り返し解いてみると良きですよ。
さて、次の記事では「等加速度直線運動の練習問題」を5つほど紹介しています。
コツや公式の使い方についても丁寧に解説していますので、ぜひチャレンジしてみてください。
↓8月9日公開予定です。本記事をブックマークしてお待ちください。

あとで読みたいあなたには「ブックマーク」がおススメだよ!
少しでも”良い記事”だと思ったら、SNSシェアもよろしくね!