連立不等式の解き方を7枚の画像で図解！共通範囲の求め方から応用問題まで

この記事では、こういった疑問に答えます。

 

 

 

連立不等式は、食塩水問題などの文章問題を解く時に利用する、一次不等式（および二次不等式）の応用テクニックです。

本記事を読めば、たった10分のうちに「連立不等式 怖くねぇ！」状態になりますので、ぜひ最後までご覧ください。

 

また、不等式の基礎知識については以下の記事でサクッと確認できます。

 

》参考：5秒で理解する不等式の性質まとめ｜高校生が必ずつまづく基礎問題付き

 

連立不等式の解き方と共通範囲について｜＋数直線の書き方も解説

 

つまづく高校生が続出する「連立不等式」ですが、難しく考える必要はありません。

解き方はシンプルでして、やるべきことは2つだけです。

 

 

本当にこれだけ。その他の難しいテクニックは必要ありません。

 

 

共通範囲とは、各不等式を解いて求められたそれぞれの解（xの値の範囲）の、「共通部分」のことです。

 

例えば次のような連立方程式があったとして、

$$\left\{%
\begin{array}{l}
x≦1・・・①\\
-5<x・・・②
\end{array}
\right.$$

 

この連立不等式の解（①と②の共通範囲）は次の通り。

$$-5<x≦1$$

 

これを数直線に表すと、

 

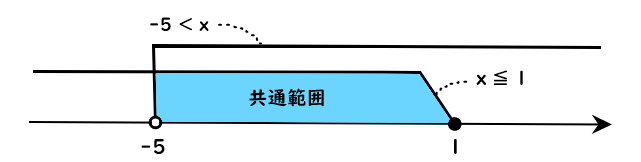
連立不等式を解く上で、「数直線」の概念はとても重要になります。

実際に図を書くにしろ、頭でイメージするにしろ、複数の不等式の共通範囲を求めるときには必ず利用するからです。

 

この記事を見ているあなたにも、”慣れるまでは”プリントの余白などに数直線を書きつつ、問題を解いていくことをおススメします。

 

では最後に、数直線を書く際のルールをサクッとまとめます！

 

 

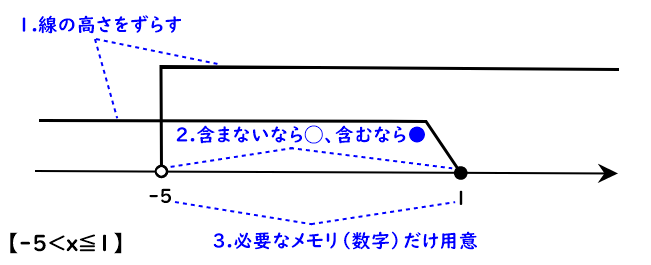
さて、次章はいよいよ実践編。

連立不等式の練習問題を3問ほど解きつつ、連立不等式の解き方をマスターしましょう。

 

連立不等式の練習問題で基礎固め！解き方の解説つき

 

ではでは、さっそく連立不等式の基礎問題を解いていきましょう。

今回用意した問題はこちら。

 

 

間違わずに解ければ、連立不等式の基礎はバッチリですよ！

 

》リターン：目次に戻る

》スキップ：応用問題を解く

その①｜連立不等式の練習問題

 

$$\left\{%
\begin{array}{l}
x-3>4x+1・・・Ⓐ\\
4(x+1)<2x+1・・・Ⓑ
\end{array}
\right.$$

 

Ⓐより、

$$-3>3x+1$$

$$-4>3x$$

$$x<-\dfrac{4}{3}$$

 

Ⓑより、

$$4x+4<2x+1$$

$$2x<-3$$

$$x<-\dfrac{3}{2}$$

 

ⒶⒷの解（xの値の範囲）を、数直線に表すと

 

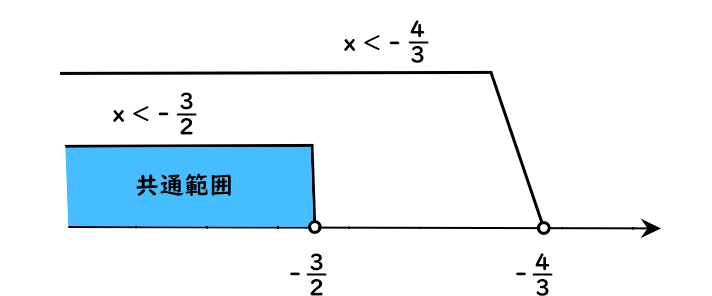
よって共通範囲は

$$x<-\dfrac{3}{2}・・・（答え）$$

 

その②｜連立不等式の練習問題

 

$$\left\{%
\begin{array}{l}
5x+1≦8(x+2)・・・Ⓐ\\
2x-3<1-(x-5)・・・Ⓑ
\end{array}
\right.$$

 

Ⓐより、

$$5x+1≦8x+16$$

$$-15≦3x$$

$$-5≦x$$

 

Ⓑより、

$$2x-3<1-(x-5)$$

$$2x-3<1-x+5$$

$$3x<9$$

$$x<3$$

 

ⒶⒷの解（xの値の範囲）を、数直線に表すと

 

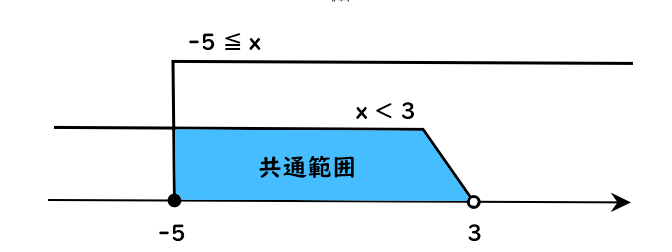
よって共通範囲は

$$-5≦x<3・・・（答え）$$

 

その③｜連立不等式の練習問題

 

$$\left\{%
\begin{array}{l}
2x+3>x+2・・・Ⓐ\\
3x>4x+2・・・Ⓑ
\end{array}
\right.$$

 

Ⓐより

$$2x-x>2-3$$

$$x>-1$$

$$-1<x$$

 

Ⓑより

$$3x-4x>2$$

$$-x>2$$

$$x<-2$$

 

ⒶⒷの解（xの値の範囲）を、数直線に表すと

 

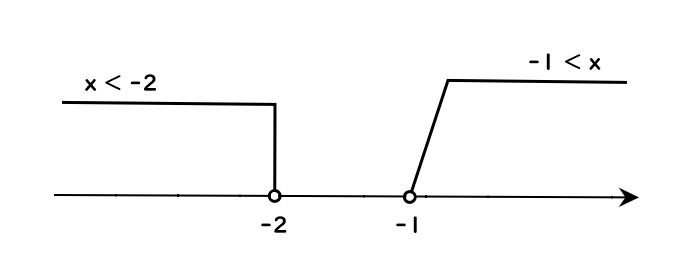
よって共通範囲は

$$なし/解なし・・・（答え）$$

 

連立不等式の応用問題にチャレンジ！テストで頻出する良問3選

 

連立不等式の基礎を固めた人は、応用問題にもチャレンジしてみましょう！

今回用意した問題はこちら。

 

 

一番難しいのは、その③で紹介した文章問題。

しかし、情報を整理しながら式を組み立てれば、解けない問題ではありません。

 

連立不等式の基礎的な解き方を意識しつつ、落ち着いて、チャレンジをどうぞ。

 

》リターン：目次に戻る

その①｜連立不等式の応用問題

 

「不等式が3つもある！？」

と驚くかもしれませんが、解き方はカンタン。

 

このような問題の場合、まずは真ん中を軸に不等式を2つに分け、連立不等式を作るところから始めます。

 

$$\left\{%
\begin{array}{l}
-2x+1<3x+4・・・Ⓐ\\
3x+4<2(3x-4)・・・Ⓑ
\end{array}
\right.$$

 

あとは先ほどと同様に、ⒶⒷそれぞれの連立不等式を解き、共通範囲を求めるだけ。

 

Ⓐより、

$$-2x+1<3x+4$$

$$1-4<3x+2x$$

$$-3<5x$$

$$-\dfrac{3}{5}<x$$

 

Ⓑより、

$$3x+4<6x-8$$

$$4+8<6x-3x$$

$$12<3x$$

$$4<x$$

 

ⒶⒷの解（xの値の範囲）を、数直線に表すと

 

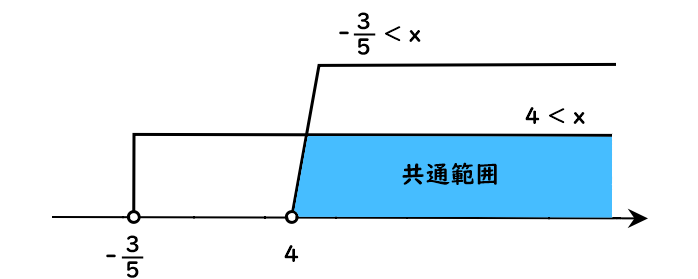
よって共通範囲は

$$4<x・・・（答え）$$

 

その②｜連立不等式の応用問題

 

この問題も、解き方は先ほどと同じ。

まずは、3つの式の真ん中を軸にして2つに分け、連立不等式を作ります。

 

$$\left\{%
\begin{array}{l}
\dfrac{4(1-x)}{3}<\dfrac{3(x-2)}{4}・・・Ⓐ\\
\dfrac{3(x-2)}{4}<\dfrac{2(1-x)}{5}・・・Ⓑ
\end{array}
\right.$$

 

Ⓐより、

$$\dfrac{4(1-x)}{3}<\dfrac{3(x-2)}{4}$$

両辺に、各分母の最小公倍数である$12$を掛けて

$$4(1-x)×4<3(x-2)×3$$

$$16-16x<9x-18$$

$$34<25x$$

$$\dfrac{34}{25}<x$$

 

Ⓑより、

$$\dfrac{3(x-2)}{4}<\dfrac{2(1-x)}{5}$$

各辺に、各分母の最小公倍数である$20$を掛けて

$$15(x-2)<8(1-x)$$

$$15x-30<8-8x$$

$$23x<38$$

$$x<\dfrac{38}{23}$$

 

ⒶⒷの解（xの値の範囲）を、数直線に表すと

 

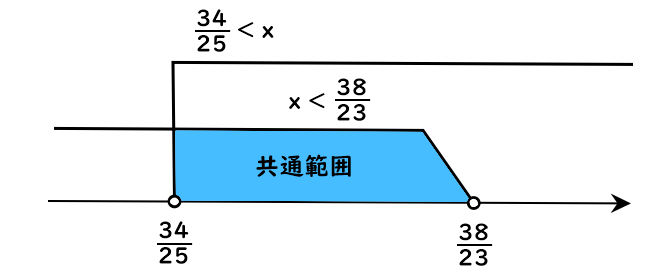
よって共通範囲は

$$\dfrac{34}{25}<x<\dfrac{38}{23}・・・（答え）$$

 

その③｜連立不等式の応用問題

 

兄が初めに持っていた本数を $x$ 本とすると、弟は $52-x$ 本持っていることになる。

 

次に、兄が弟に自分が持っているペンの $\dfrac{1}{3}$ をあげても、まだ兄の方が多いことから、次の式が成立する。

$$(52-x)+\dfrac{x}{3}<x-\dfrac{x}{3}・・・Ⓐ$$

$$弟の本数 + 貰った本数 < 兄の本数 – あげた本数$$

 

続いて、更に3本あげると弟の方が多くなることから、次の式が成立する。

$$(52-x)+\dfrac{x}{3}+3<x-\dfrac{x}{3}-3・・・Ⓑ$$

 

ⒶとⒷを連立方程式としてそれぞれ解くと

$$\left\{%
\begin{array}{l}
(52-x)+\dfrac{x}{3}<x-\dfrac{x}{3}・・・Ⓐ\\
(52-x)+\dfrac{x}{3}+3<x-\dfrac{x}{3}-3・・・Ⓑ
\end{array}
\right.$$

 

ーⒶより、

$$52<2(x-\dfrac{x}{3})$$

$$26<\dfrac{2x}{3}$$

$$39<x$$

 

―Ⓑより、

$$52+6>2(x-\dfrac{x}{3})$$

$$29>\dfrac{2x}{3}$$

$$x<43.5$$

 

ⒶとⒷより、xの値は $39<x<43.5$ を満たす整数であるから、

$40,$ $41,$ $42$

 

この中で、ぴったり $\dfrac{1}{3}$ に分けて（弟に）あげられるものは

$$42 だけである・・・（答え）$$

 

連立不等式の解き方まとめ

 

以上で、「連立不等式の解き方」についての解説は終了です。

 

連立不等式を攻略するコツは、なんといっても数直線。

常に数字や文字の大小関係を意識しつつ、正確に共通範囲を導き出せるようにしましょうね。