- 二次関数を対象移動する方法
- x軸に関して対称移動:$y=-f(x)$
例:$y=x^2+2x+3$ → $\color{blue}y=-(x^2+2x+3)$
- y軸に関して対称移動:$y=f(-x)$
例:$y=x^2+2x+3$ → $\color{blue}y=(-x)^2+2(-x)+3$
- 原点に関して対称移動:$y=-f(-x)$
例:$y=x^2+2x+3$ → $\color{blue}y=-\left[(-x)^2+2(-x)+3\right]$



- 本日の授業内容
- x軸に関して対称移動する方法
- y軸に関して対称移動する方法
- 原点に関して対称移動する方法
- 対称移動の練習問題を解いてみよう
ここからは「なぜ上の公式が成り立つのか?」をわかりやすく解説していきます。
対称移動の公式の仕組みはとても簡単ですし、二次関数の根本理解にもつながります。

高校1年生の方は、今後も二次関数・二次方程式・二次不等式....と、なにかと二次式にお世話になります。
ぜひこの記事を最後まで読んで、二次関数分野攻略の糸口をつかんでください!
二次関数グラフをx軸に関して対称移動する方法
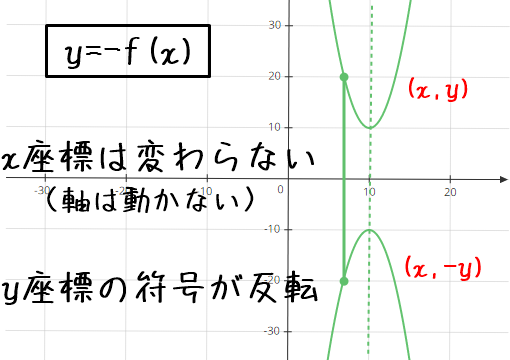
- 対称移動の注目ポイント(x軸 ver)
- x座標は変化しない(軸は動かない)
- y座標の符号が反転
この2点を、実数を使って確認してみましょう。
二次関数の頂点に注目すると、理解しやすいと思いますよ。
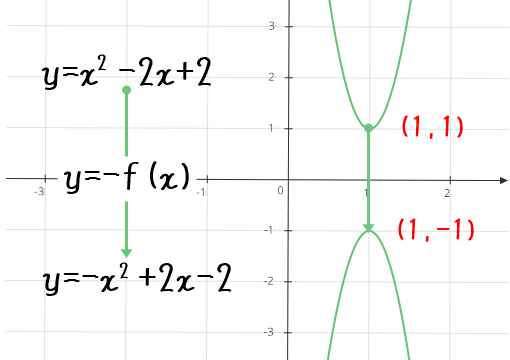
二次関数グラフというのは、いわば「点の集合体」です。
ゆえに、グラフ上の一点(例えば頂点)が、x軸に関して対称移動すれば、グラフ上のその他の点も同じように移動します。



まさにそのとおりです!
x軸に関して対称移動する場合は、x座標は変化せず、y座標の符号が反転するので
$$\color{red}-y\color{black}=f(x)$$
$$\color{red}y=-f(x)$$
※$f(x)はxの関数部分(例:x^2+2x+2)を意味する$
といった具合に、公式が導き出されるわけですね。
二次関数グラフをy軸に関して対称移動する方法
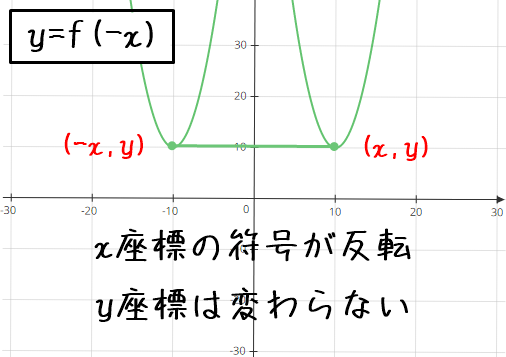
- 対称移動の注目ポイント(y軸 ver)
- x座標の符号が反転
- y座標は変化しない
この2点を実数を使って確認してみましょう。
ここでもまた二次関数の「頂点」に注目することで、スッと理解できますよ。
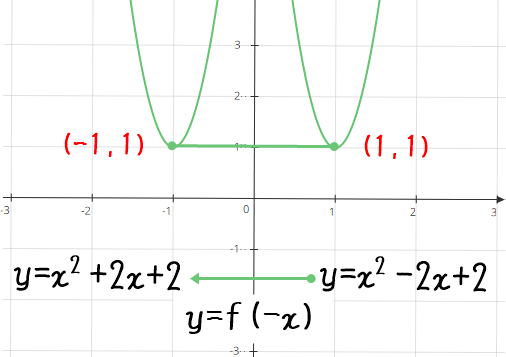
y軸に関して対称移動する場合は、y座標は変化せず、x座標の符号が反転するので
$$y=f(\color{red}-x\color{black})$$
$$\color{red}y=f(-x)$$
※$f(-x)は関数に-xを代入するという意味$
二次関数グラフを原点に関して対称移動する方法
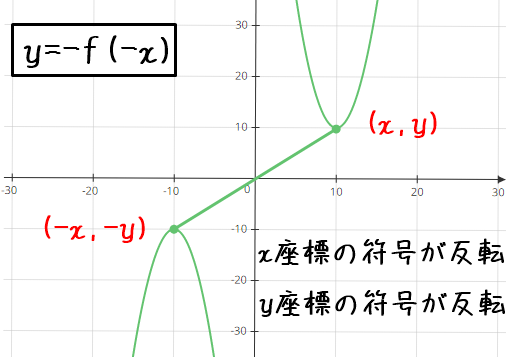
- 対称移動の注目ポイント(原点 ver)
- x座標の符号が反転
- y座標の符号も反転
要は、ここまでに紹介した「x軸対称移動」と「y軸対称移動」を、それぞれ1回ずつすればOK。というわけです。
これも、二次関数の頂点に注目することで理解しやすくなりますよ。
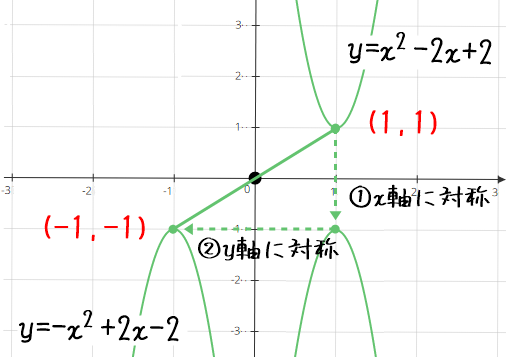
原点に関して対称移動する場合は、y座標もx座標も符号が反転するので
$$\color{red}-y\color{black}=f(\color{red}-x\color{black})$$
$$\color{red}y=-f(-x)$$
以上で、対象移動の方法についての解説は終了です。
今日覚えたことをしっかりと定着させたい方は、ぜひ、下で紹介している「練習問題」も解いてみてください!


- 【二次関数】対象移動の公式まとめ
- x軸に関して対称移動→$\color{blue}y=-f(x)$
- y軸に関して対称移動→$\color{blue}y=f(-x)$
- 原点に関して対称移動→$\color{blue}y=-f(-x)$
【二次関数】対象移動の練習問題を解いてみよう
$y=x^2+2x+5$ を以下のように移動したとき、移動後の式を求めよ。
①x軸に関して対称移動
②y軸に関して対称移動
③原点に関して対称移動
①$y=-x^2-2x-5$
②$y=x^2-2x+5$
③$y=-x^2+2x-5$
問題解説|x軸に関して対称移動
x軸に関して対称移動する公式は $\color{blue}y=-f(x)$ なので、
$$y=-(x^2+2x+5)$$
$$y=-x^2-2x-5\color{red}(答え)$$
問題解説|y軸に関して対称移動
y軸に関して対称移動する公式は $\color{blue}y=f(-x)$ なので、
$$y=(-x)^2+2(-x)+5$$
$$y=x^2-2x+5\color{red}(答え)$$
問題解説|原点に関して対称移動
原点に関して対称移動する公式は $\color{blue}y=-f(-x)$ なので、
$$y=-\left[(-x)^2+2(-x)+5\right]$$
$$y=-(x^2-2x+5)$$
$$y=-x^2+2x-5\color{red}(答え)$$
二次関数の対象移動を理解したなら、お次は「平行移動」へ進みましょう。



》参考:二次関数をたった3行で平行移動する方法|頻出問題の解き方も解説