


- 本記事の内容
二次関数のグラフを速攻で書く手順
- 二次関数のグラフに必要な情報
- 原点
- 頂点座標
- グラフの軸
- x軸とグラフの交点(x切片)
- y軸とグラフの交点(y切片)
ぶっちゃけ、上記5つの情報が明確に示されていれば、グラフの書き方はなんでもOK。
ただし今回は、より効率的に二次関数のグラフを書く手順を紹介します。
手順は全部で5つあります。
- 二次関数のグラフの書き方
- 手順①:平方完成で頂点の「座標」「軸」を求める
- 手順②:$x^2$ の係数を確認し「上凸」か「下凸」かを判断
- 手順③:ここまでで分かったことを図に表す
- 手順④:「頂点」と「y軸」の関係を図に書き込む
- 手順⑤:「頂点」と「x軸」の関係を図に書き込む

二次関数のグラフは、慣れれば10秒ほどで書けるようになりますよ!
ここからは以下の二次関数を使って、グラフの書き方を解説していきます。
$${\large y=x^2+6x+8}$$
手順①:平方完成で頂点の「座標」「軸」を求める
$${\large y=x^2+6x+8}$$
まずは二次関数の頂点座標と軸を求めていきます。
平方完成を使ってもよし、公式を利用してもよしなので、お好きな方法を選択してください。
【平方完成する方法】
$$y=x^2+6x+8$$
$$=(x+3)^2-9+8$$
$$=(x+3)^2-1$$
よって頂点、軸はそれぞれ
$$\color{red}頂点\color{black}:(-3,-1)$$
$$\color{red}軸\color{black}:x=-3$$
【公式を利用する方法】
$y=ax^2+bx+c$ の頂点のx座標(軸)が次のように表されることを利用する。
$$x=-\dfrac{b}{2a}$$
よって、軸は
$$x=-\dfrac{6}{2(1)}$$
$$\color{red}軸\color{black}:x=-3$$
$x=-3$ を $y=x^2+6x+8$ に代入すると
$$y=(-3)^2+6(-3)+8$$
$$y=-1$$
よって頂点座標は
$$\color{red}頂点\color{black}:(-3,-1)$$
手順②:二次の係数を確認し「上凸」か「下凸」かを判断
$${\large y=x^2+6x+8}$$
続いては $x^2$ の係数を確認し、グラフの向きが「上凸」か「下凸」かを判断します。
今回の場合、$x^2$ の係数は $1$ ですので、グラフの向きは「下凸」ですね!

手順③:ここまでで分かったことを図に表す
ここからは、いよいよ実際にグラフを書いていきます。
ここまでに分かっている情報は次の通り。
- 頂点座標は $(-3,-1)$
- グラフの軸は $x=-3$
- グラフの向きは下凸
これらの情報を図に表すと、、、
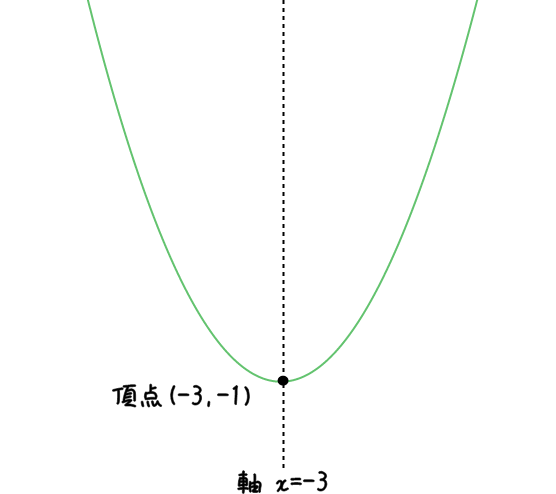



手順④:「グラフとy軸」の関係を図に書き込む
続いては、グラフとy軸の関係を先ほどの図に書き込んでいきます。
【書き込む情報】
- グラフとy軸の交点(y切片)の位置
- グラフの軸とy軸の大小関係
y切片の座標は、$y=x^2+6x+8$ に $x=0$ を代入することで求められます。
$$y=(0)^2+6(0)+8$$
$$y=8\color{red}(y切片)$$
グラフの軸は $x=-3$、y軸は $x=0$ だから、両者の大小関係は
$$グラフ軸<y軸\color{red}(大小関係)$$
以上2つの情報をグラフに書き込むと、、、

手順⑤:「グラフとx軸」の関係を図に書き込む
最後に、グラフとx軸の関係を先ほどの図に書き込んでいきます。
【書き込む情報】
- グラフとx軸の交点(x切片)の位置
- 頂点のy座標とx軸の大小関係
x切片の座標は、$y=x^2+6x+8$ に $y=0$ を代入することで求められます。
$$0=x^2+6x+8$$
$$0=(x+2)(x+4)$$
$$x=-2,-4\color{red}(x切片)$$
頂点のy座標は $y=-1$、x軸は $y=0$ だから、両者の大小関係は
$$頂点のy座標<x軸\color{red}(大小関係)$$
以上2つの情報をグラフに書き込むと、、、

これで二次関数グラフの完成です。
グラフの書き方をまとめると、こんな感じ。
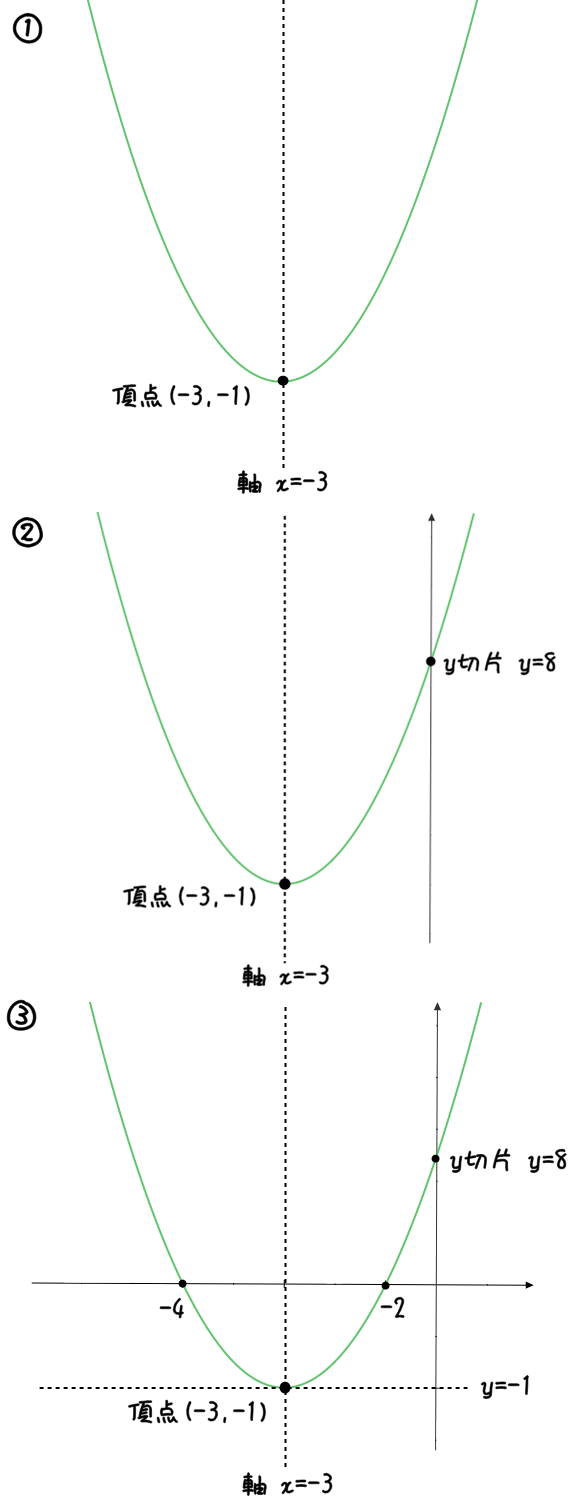
二次関数のグラフの書き方|x軸とy軸は最後に書こう
今回用意した二次関数のグラフ問題は2つ。
ぜひ、いったんここでスクロールを止めて、問題にチャレンジしてみてください!

- 二次関数のグラフを書いてみよう
- 練習問題①
$y=-2x^2+x+1のグラフを書きなさい。$ - 練習問題②
$y=ax^2+bx+cのグラフが下図のように表されるとき、次の式の符号を求めなさい。$
$(1)a$
$(2)b$
$(3)c$
$(4)a+b+c$
$(5)a-b+c$
$(6)b^2-4ac$

練習問題①の解説
まずは、頂点の座標と軸を求めよう。
今回は平方完成で頂点座標を求めるが、公式を利用して求めてもOK。(公式解説)
$$y=-2x^2+x+1$$
$$=\color{red}-2\left(x^2-\dfrac{1}{2}x\right)\color{black}+1$$
$$=-2\color{red}\left(x-\dfrac{1}{4}\right)^2+2\left(\dfrac{1}{4}\right)^2\color{black}+1$$
$$=-2\left(x-\dfrac{1}{4}\right)^2\color{red}+\dfrac{9}{8}$$
よって頂点と軸はそれぞれ
$$頂点:\left(\dfrac{1}{4},\dfrac{9}{8}\right)$$
$$軸:x=\dfrac{1}{4}$$
次に $x^2$ の係数を確認し、グラフの向きが「上に凸」か「下に凸」かを判断する。
今回、$x^2$ の係数は $-2$ だから、$y=-2x^2+x+1$ は上に凸のグラフであることが分かる。
以上の情報を図に表すと、こうなる。



今の段階で書き込むと、あとから修正する必要も出てきてしまいますので!
ここまでくれば、あとは上記の図に「x軸」「y軸」との関係を書き込めばいい。
- $x=0$ のとき $y=1(y切片=1)$
- 頂点のx座標は正の数
- 頂点のy座標は正の数
この3点をグラフに書き込むと、こうなる。
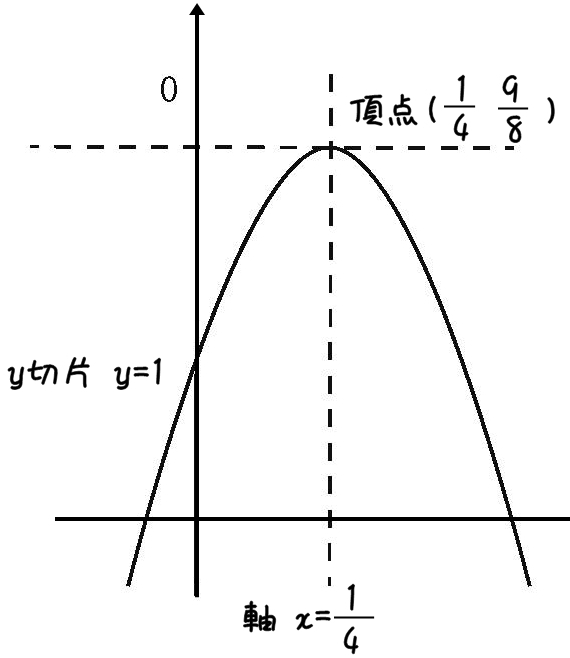


どうしても、x軸 y軸を先に書きたくなっちゃう。

ただ、上凸下凸を確認してからでも遅くないし、その方が効率的だってことは覚えておこうね!
練習問題②の解説
$y=ax^2+bx+cのグラフが(A)のように表されるとき、次の式の符号を求めなさい。$
$(1)a$
$(2)b$
$(3)c$
$(4)a+b+c$
$(5)a-b+c$
$(6)b^2-4ac$
$(1)a>0$
$(2)b<0$
$(3)c<0$
$(4)a+b+c=0$
$(5)a-b+c>0$
$(6)b^2-4ac>0$
(1)の解説

下に凸のグラフだから、$a$ の値はプラスということになる。
$$a>0\color{red}(答え)$$
(2)の解説
軸の公式より、グラフの軸は次のように表せる
$$x=-\dfrac{b}{2a}$$
図を見ると「y軸<グラフの軸」という関係性が分かるため、
$$-\dfrac{b}{2a}>0$$
よって
$$b<0\color{red}(答え)$$
(3)の解説
$c$ はy切片であり、y切片は原点より下にあるため
$$c<0\color{red}(答え)$$

なんで $c$ がy切片になるんですか?

(4)の解説
問題のグラフを見てみると、グラフとx軸との交点(x切片)が $(1,0)$ であることが分かる。
$y=ax^2+bx+c$ に $x=1$ を代入すると
$$y=a(1)^2+b(1)+c$$
$$=a+b+c$$
$y=0$ であるから、すなわち
$$a+b+c=0\color{red}(答え)$$
(5)の解説
先ほどは $x=1$ を代入したが、今回は $x=-1$ を代入して答えを求めていく。
$y=ax^2+bx+c$ に $x=-1$ を代入すると
$$y=a(-1)^2+b(-1)+c$$
$$=a-b+c$$
ここでグラフをみると、$x=-1$ の位置は明確に示されていないことが分かる。
しかし、原点と $x=1$ の距離感から、大体の位置を推測することができる。
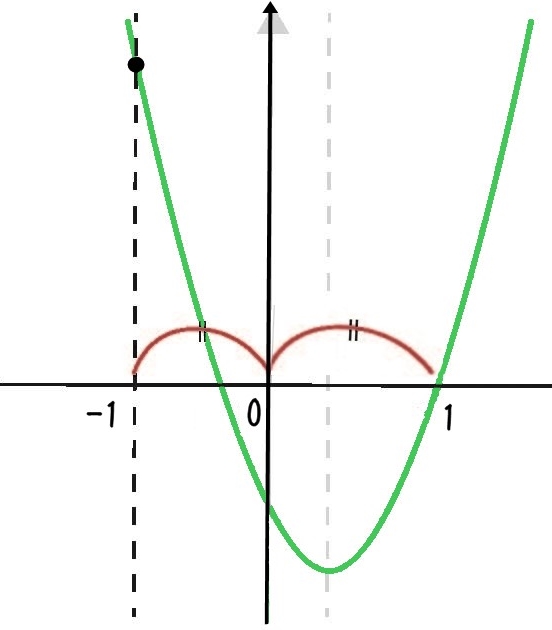
上の図より、$x=-1$ の時 $y>0$ であることが分かるから
$$a-b+c>0\color{red}(答え)$$
(6)の解説
$y=ax^2+bx+c$ を平方完成すると、頂点座標は次のように表せる。
$$\left(-\dfrac{b}{2a},\color{red}-\dfrac{b^2-4ac}{4a}\color{black}\right)$$

》参考:平方完成を10秒で終わらせるコツと方法|基本+簡単なやり方を解説
グラフを見ると、頂点のy座標が負であることが分かるから、
$$-\dfrac{b^2-4ac}{4a}<0$$
$$\dfrac{b^2-4ac}{4a}\color{red}>\color{black}0$$
(1)より $a>0$ であるから、両辺に $4a$ を掛けて
$$b^2-4ac>0\color{red}(答え)$$
また別解として、(1)(2)(3)で明らかになった$a,$ $b,$ $c$ の符号を $b^2-4ac$ に当てはめることでも、答えが求められる。
$$(負)^2-4(正)(負)>0$$
まとめ|二次関数グラフの書き方
以上で、今回の授業は終了だ。
今回紹介した2つの問題(特に2問目)は、高校の先生が校内模試などで頻繁に出題する問題の一つだ。
この記事を何度も復習したり類似問題を解くことで、二次関数に対する理解がより深まり、効果的な試験対策になることは間違いないだろう。